Grundlagen

Die Daten wurden in einer Exeldatei ausgegeben. Zu Beginn sortierte ich alle unvollständigen Fragebögen aus. Anschließend überprüfte ich alle Fragebögen auf Plausibilität. Einige Daten konnte ich nicht verwenden, da sich der Chronotyp nicht berechnen lässt wenn an allen Tagen der Woche ein Wecker verwendet wird. Schließlich blieben 155 Datensätze übrig, die ich zur Auswertung heranziehen konnte.

Für die statistische Auswertung nutzte ich als Grundlage die 7. Auflage des Buches “Angewandte Statistik” von Lothar Sachs, erschienen 1992 im Springer-Verlag.

Zunächst werde ich meine Daten auf Normalverteilung mittels Χ²-Anpassungstest prüfen. “Ein Anpassungstest prüft die Nullhypothese (H0): F(x)=F0(x) gegen die Alternativhypothese: F(x)≠F0(x).” (S. 420). Prüft man auf Normalverteilung sollte die Stichprobenanzahl 60 nicht unterschreiten. Weiterhin sollte es mindestens 7 Kategorien geben. Dabei sollten pro Kategorie mindestens 2 Werte vorhanden sein. Sonst werden diese Kategorien mit einer benachbarten Kategorie zusammengeführt.

Der Test führt eine Prüfgröße X̂² ein, welche kleiner sein sollte, als X̂². α bezeichnet dabei das Wahrscheinlichkeitsniveau auf dem geprüft wird.

Zur Berechnung vonwerden folgende Werte benötigt:

  • k – Anzahl der Klassen
  • b – Klassenbreite
  • v – Freiheitsgrad ( v=k-1)
  • Bi – beobachtete Häufigkeit einer Kategorie
  • Pi – Wahrscheinlichkeit dafür, dass ein zufälliger Wert in der Kategorie i liegt
  • Ei=n*pi – ist demnach die erwartete Häufigkeit der Kategorie i.

Nun kann man X̂² wie folgt darstellen:

\sum^k_{i=1}\frac{(B_i-E_i)^2}{E_i}=\sum^k_{i=1}\frac{B_i^2}{E_i}-n \qquad \text{bzw.} \\ \sum^k_{i=1}\frac{(n_i-np_i)^2}{np_i}=\sum^k_{i=1}\frac{n_i^2}{p_i}-n

Um gegen eine Normalverteilung zu prüfen benötigt man noch die Standardnormalverteilungsvariable z. z ist demnach die Funktionsvariable der Standardnormalverteilungsfunktion:

f(z) =\frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}

Für einen bestimmten Wert x kann mit Mittelwert und Standardabweichung z und damit auch f(z) berechnet werden. In der Auswertung wird außerdem noch K verwendet, welches multipliziert mit der Wahrscheinlichkeit die erwartete Häufigkeit ergibt.

E=f(\hat{z})*K \quad\text {mit} \quad K = nb/s

In der zweiten Frage verbirgt sich die Frage nach Konvergenz. Ich werde allerdings nur den Korrelationskoeffizient berechnen und die Steigung der Regressionsgeraden.

Ich möchte n Wertepaare der Form (Xi|Yi) auf Konvergenz prüfen. Dazu betrachtet man nur die Differenzen der Koordinaten zu deren Mittelwert. Nun summiere ich das Produkt der X-Differenz und der Y-Differenz auf und teile es durch die Wurzel aus dem Produkt der Summen der Quadrate der Differenzen. Allgemein wird r wie folgt ausgedrückt:

r=\frac{\sum \Delta x_i \Delta y_i}{\sqrt{\sum\Delta x^2_i \sum \Delta y^2_i}}

Der Korrelationskoeffizient ist ein Maß für die Stärke einer Linearen Abhängigkeit. Um das Rechnen zu vereinfachen, kann man ihn umformen zu

r=\frac{\sum \Delta x_i \Delta y_i}{\sqrt{\sum\Delta x^2_i \sum \Delta y^2_i}} = \frac{\sum (X_i-\bar X)(Y_i-\bar Y)} {\sqrt{\sum(X_i-\bar X)^2 \sum (Y_i-\bar Y)^2}} =\frac{\sum XY- \frac{1}{n}(\sum X)(\sum Y)}{\sqrt {(\sum X^2 – \frac{1}{n}[\sum X]^2)\left(\sum Y^2 – \frac{1}{n} [\sum Y]^2\right)}}

Benötigt werden jetzt nur noch:

\sum X; \sum X^2; \sum Y; \sum Y^2; \sum XY

Als letztes statistisches Mittel nutze ich den t-Test. Dieser einfache Test prüft das sogenannte Fisher-Behrens-Problem, also ob zwei Mittelwerte gleich sind, bei ungleichen Varianzen. (Vgl. Sachs 1992, S.355). Die Prüfgröße ist dabei t. Geprüft wird gegen die Studentverteilung.

t = \frac {|\bar x_1 – \bar x_2|}{\sqrt {\frac {s^2_1}{n_1}+\frac{s^2_2}{n_2}}}

Wenn der Stichprobenumfang ausreichend groß ist, kann man auch gegen die Standardnormalverteilung prüfen, also gegen z.

Ergebnisse

Da die meisten statistischen Tests eine normalverteilte Grundgesamtheit voraussetzen, prüfe ich zunächst auf Normalverteilung. Ich nutze dazu den X2-Anpassungstest.

xBBxBx²x-x̅ẑf(ẑ)E=f(ẑ)*KB-E(B-E)²/E
1:00333-2,922,060,04785,229-2,2290,950
2:00163264-1,921,350,160417,546-1,5460,136
3:0045135405-0,920,630,327135,76910,2312,926
4:00471887520,080,050,398443,5793,4210,269
5:00271356751,080,730,305633,428-6,4281,236
6:009543242,081,410,147616,145-7,1453,162
7:005352453,082,100,04404,8130,1870,007
8:0018644,082,780,00841,0281,9723,783
9:002181625,083,460,0010^
Σ1556082694204,595-48,595X̂²=12,469
\bar x = \frac{\sum Bx}{n}=\frac{608}{155}=3.92
s= \sqrt {\frac{\sum Bx^2-\frac {(\sum Bx)^2}{n}}{n-1}}=\sqrt{\frac{2694-\frac{608^2}{155}}{154}}=1.417
K=\frac{nb}{s}=\frac{155*1}{1.417}=109.386
\hat X^2=12.469 < 14,07 = X^2_{0.05}

Damit ist gegen die Normalitätshypothese nichts einzuwenden. Die Daten können also annähernd normalverteilt angenommen werden und die Grundgesamtheit als normalverteilt.

So wie der Chronotyp sollten auch natürliche Aufwach- und Einschlafzeit normalverteilt sein. Deswegen habe ich auch diese Größen auf Normalverteilung untersucht und kam zu folgendem Ergebnis:

natürliche EinschlafzeitChronotypnatürliche Aufwachzeit
Anzahl Klassen787
Mittelwert23:59 Uhr3:55 Uhr7:54 Uhr
Standardabweichung1,79h1,42h1,20h
X²5,9212,4698,62
Satistische Signifikanz50%95%90%

Die statistische Signifikanz der Einschlafzeit war überraschend gering. Wahrscheinlich wird die Normalverteilung durch sekundäre Faktoren verzerrt, die ich zur Zeit nicht überblicken kann (Abendessen mit der Familie, Training im Verein…). Für die natürliche Aufwachzeit dagegen kann ich die Normalitätshypothese annehmen.

Nun gibt es noch weitere Größen: Schlafdauer, persönliche Zeit am Morgen und Schulweg sind alle nach unten begrenzt. Keine der Größen kann kleiner 0 werden. Deswegen können diese Größen nicht normalverteilt sein. Wahrscheinlicher ist eine logarithmische Normalverteilung. Da die meisten statistischen Tests aber eine annähernde Normalverteilung voraussetzen, habe ich trotzdem überprüft, ob ich diese Größen vereinfachend als annähernd normalverteilt voraussetzen kann.

SchlafdauerPersönliche Zeit am MorgenSchulweg
Anzahl Klassen678
Mittelwert7:58h68,84 min29,74
Standardabweichug1,24h23,82 min17,44 min
X²5,843,289,17
Statistische Signifikanz70%70%80%

Man sieht, dass es sich um keine exakten Normalverteilungen handelt. Während ich den Schulweg noch als annähernd normalverteilt annehmen kann, kann ich das für die Schlafdauer und die persönliche Zeit am Morgen nicht.

1. Beginnt die Schule zu zeitig? Und wenn ja, was wäre ein optimaler Schulbeginn?

Als optimalen Schulbeginn lege ich die früheste Zeit fest, zu der ein Schüler ausgeschlafen in der Schule sein kann.

Dazu berechne ich für jeden Teilnehmer die Summe aus natürlichem Aufwachzeitpunkt und Dauer des Schulwegs. In der Woche ist zwischen Aufwachzeitpunkt und Schulbeginn minus Dauer des Schulwegs im Durchschnitt noch eine Stunde Differenz. Diese wird zum Frühstücken, im Bad oder in der Schule zur Vorbereitung auf den Unterricht genutzt. Ich nenne diese Zeit „persönliche Zeit am Morgen“. Ich vermute, dass diese Zeit sich ändern würde, würde die Schule zu einer anderen Zeit beginnen. Zum Beispiel bräuchten manche Schüler bei einem zeitigerem Beginn dann länger, um munter zu werden, andere würden lieber länger schlafen als zu frühstücken.

Genauso kann man auch einen Zusammenhang zwischen Schulweg und Chronotypen vermuten. Schüler, die eine späten Chronotypen haben nehmen lange Schulwege vielleicht nicht so gerne in Kauf wie Menschen mit einem zeitigem Chronotyp. Dafür gehen Schüler mit einem späten Chronotypen, die in der Nähe der Schule wohnen lieber auf unsere Schule als einen längeren Weg zu einer anderen. So ließen sich auf jeden Fall Zusammenhänge erklären.

Um diese Fehler zu vermeiden betrachte ich zunächst verschiedene Varianten. Einmal nehme ich für jeden Schüler unverändert die Zeit, die er bisher brauchte vom Aufstehen bis zum Schulbeginn. Dieser Fall gilt auch kurzfristig für die Zukunft. Einmal rechne ich mit dem individuellem Schulweg wie bisher, aber berechne für die persönliche Zeit am Morgen den Durchschnitt (ca. 67 min) und wende diese auf alle an. Diese Variante gilt eher mittelfristig, da die Schüler auch in den nächsten Jahren denselben Schulweg zu bewältigen haben. In der letzten Variante rechne ich für alle Schüler mit dem allgemeinen Durchschnitt der persönlichen Zeit und des Schulwegs (ca. 1h 34 min). Auch hier vereinfache ich zu 1:30h. Die letzte Variante bietet die besten langfristigen Prognosen, da neue Schüler eingeschult werden und alte Schüler entlassen. Damit ändern sich auch die Schulwege.

Möglich wäre, dass bei späterem Schulbeginn Schüler, welche weiter entfernt wohnen, sich doch für unsere Schule entscheiden. Dadurch könnte sich der Durchschnitt des Schulweges insgesamt erhöhen. Andererseits gelten Bestimmungen der Schulbehörde, welche ich nicht überblicke, welcher Schüler in welche Schule eingeschult werden darf. So bleibt mir nicht anderes übrig, als von den aktuellen erhobenen Daten auszugehen.

Variante A: Ich nehme für alle Schüler die durchschnittliche persönliche Zeit am Morgen an. Der Schulweg bleibt der individuelle Wert. Die Verteilung sieht wie folgt aus:

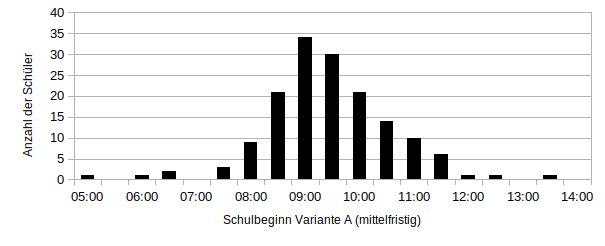
In der Variante B übernehme ich die Zeit, die ein Schüler bisher gebraucht hat vom Aufstehen bis zum Schulbeginn und addiere sie zu der natürlichen Aufwachzeit. Dann ergibt sich folgende Verteilung:

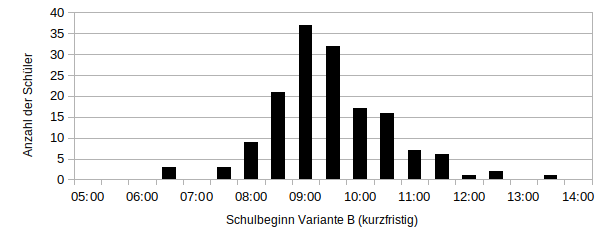
Die Variante C nimmt nur die Verteilung der Aufwachzeit und verschiebt sie um den Durchschnitt der Schulwege (~30min) sowie der persönlichen Zeit am Morgen (~1h):

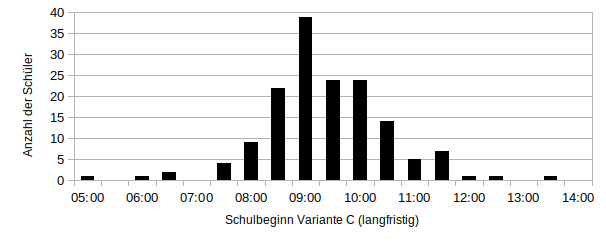
Die Variante C hat den Vorteil, dass nur die natürliche Aufwachzeit verschoben wurde. So handelt es sich hier weiterhin um eine Normalverteilung, für die ich eine Funktion angeben kann.

Die Verteilungen sehen auf dem ersten Blick sehr ähnlich aus. Mit Mittelwert und Standardabweichung, kann man die Kurven sehr gut vergleichen. Um auf die Forschungsfrage zurück zu kommen, ob die Schule zu zeitig beginnt, ermittele ich außerdem den Prozentsatz an Schülern, die 7:35 Uhr oder eher bereit für die Schule wären. Als gute Größe um Ausreißerwerte zu vernachlässigen wird der Median statt des Mittelwertes genutzt.

Variante AVariante BVariante CVariante C*
Mittelwert9:26 Uhr9:26 Uhr9:26 Uhr9:28 Uhr*
Standardabweichung1h 5 min1h 9 min1h 9 min1h 12 min*
Teilnehmer, die 7:35 Uhr bereit sind645
Prozentsatz3,8%2,8%3,2%5,8%
Median9:22 Uhr9:21 Uhr9:17 Uhr
*Diese Werte wurden aus der Normalverteilungsfunktion berechnet, gegen die zu Anfang mit dem dem Χ²Anpassungstest geprüft wurde.

Egal, welche Variante ich wähle, es wird klar, dass die Schule deutlich zu zeitig anfängt. Einen optimalen Schulbeginn gibt es nicht. Am besten wäre es natürlich, die Schule würde zwischen der spätesten Aufwachzeit und der frühesten Einschlafzeit liegen. Das wäre zwischen 12 (+Schulweg) und 21 (-Schulweg) Uhr. Da aber in der Gesellschaft verankert ist, dass die Schule vormittags beginnt, damit nachmittags und abends Zeit für Hobbys ist, wird dieser Plan schwierig. Ein Kompromiss wäre sicherlich der Median, also die Schule ungefähr um 10 vor halb 10 beginnen zu lassen. Realistisch ist das allerdings immer noch nicht. Im sächsischen Schulgesetz (Schulordnung Gymnasien Abiturprüfung § 19 Absatz 2) ist der Schulbeginn zwischen 7 und 9 vorgeschrieben. Damit wäre aus biologischer Sicht 9:00 Uhr am besten. Bezieht man noch den ÖPNV ein, wäre zunächst 8:35 Uhr anzustreben, da das für unsere Schule kaum einen Unterschied macht, weil die allermeisten Busse, Bahnen und Züge mindestens stündlich fahren.

2. Fällt es einem Teenager mit zunehmendem Alter immer schwerer, zeitig aufzustehen?

Für die Schätzung einer Regressionsgerade werden zunächst die Wertepaar in ein Koordinatensystem eingetragen.

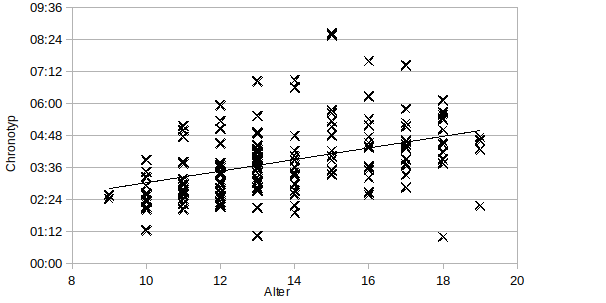
Man erkennt eine Punktwolke mit linearer Tendenz. Die Stärke kann mit dem Korrelationskoeffizient r ausgedrückt werden.

r=\frac{\sum (X_i-\bar X)(Y_i-\bar Y)}{\sqrt{\sum(X_i – \bar X)^2 \sum(Y_i-\bar Y)^2}} = \frac {\sum XY – \frac {1}{n}(\sum X )(\sum Y )} {\sqrt{(\sum X^2-\frac{1}{n}(\sum X)^2)(\sum Y^2 -\frac{1}{n} (\sum Y)^2) } }

mit X = Alter und Y = Chronotyp

Aus den Daten ergibt sich:

\sum X= 2163; \qquad \sum X^2=31181 \\ \sum Y= 25.15; \qquad \sum X^2=4.575 \\ \sum XY = 360.033 \quad \text{Einheit der Chronotyps: 1 Tag}

Nach einsetzen erhält man

r=\frac{360.033 – \frac{1}{155}*2163*25.15}{\sqrt{(31181-\frac{1}{155}*2163^2)(4.575-\frac{1}{155}*25.15^2)}} =\frac{9.9069}{\sqrt{996.684*0,494}} \approx 0,41

Damit liegt ein stochastischer linearer Zusammenhang mittlerer Stärke vor. Die Art der linearen Abhängigkeit wird durch bYX vorgegeben.

b_{yx}=\frac{\sum (X_i – \bar X)(Y_i – \bar Y)}{\sum (X_i – \bar X)^2}=\frac{\sum XY – \frac{1}{n}\sum X\sum Y}{\sum(X_i – \bar X)^2} = \frac {9.069}{996.684} \approx 0.0091\text{d}=13.1\text{min}

Das bedeutet, der Chronotyp verschiebt sich mit zunehmendem Alter in der Jugend um durchschnittlich 13,1 Minuten nach hinten pro Jahr.

Spannend ist aber nicht alleine der Chronotyp. Denn wenn sich die Schlafdauer verkürzt, könnte es sein, dass dieser Effekt gar keine Rolle spielt. Deswegen betrachte ich nun die biologische Aufwachzeit in Abhängigkeit des Alters.

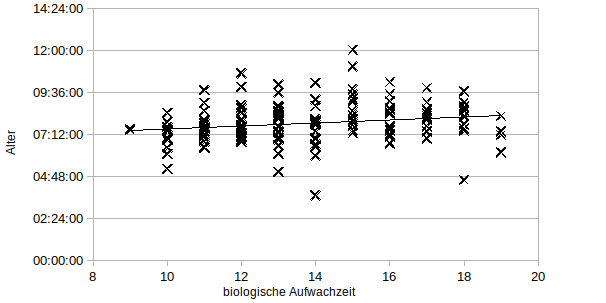
Die Punktwolke ist dichter, dafür scheint die lineare Abhängigkeit deutlich geringer zu sein. Ich berechne erneut r und bYX mit X = Alter und Y = biologische Aufwachzeit. Aus den Umfrage Daten erhält man:

\sum X= 2163; \qquad \sum X^2=31181 \\ \sum Y= 50.87; \qquad \sum X^2=17.05 \\ \sum XY = 713.433 \quad \text{Einheit der Chronotyps: 1 Tag}
r=\frac{713.433 – \frac{1}{155}*2163*50.87}{\sqrt{(31181-\frac{1}{155}*2163^2)(17.05-\frac{1}{155}*50.87^2)}} =\frac{3.5504}{\sqrt{996.684*0,355}} \approx 0,189

Hier liegt nur noch stochastische Abhängigkeit schwacher Stärke vor.

b_{yx}= \frac {3.5504}{996.684} \approx 0.0036\text{d}=5.1\text{min}

Das bedeutet mit zunehmendem Alter wachen Jugendliche um durchschnittlich 5,1 Minuten später auf pro Jahr. Das würde für Zwölftklässler einen späteren Unterichtsbeginn von ca. 30 min rechtfertigen. Praktisch lässt sich so eine kleine Differenz im Schulalltag nicht berücksichtigen. Man kann aber für die Oberstufe statt der 1. Stunde lieber am Nachmittag noch eine Stunde länger unterrichten. In eine Empfehlung für die Schule würde ich dies aber nicht mit einbeziehen, da ein allgemeiner späterer Schulanfang viel mehr Nutzen bringt als diese Berücksichtigung der altersspezifischen Unterschiede.

3. Gibt es einen Unterschied zwischen Mädchen und Jungen bezüglich der Schlafenszeiten?

Zunächst trenne ich die Stichproben nach männlich und weiblich. Ich erhalte nun zwei Verteilungen, deren Mittelwerte ich vergleichen möchte.

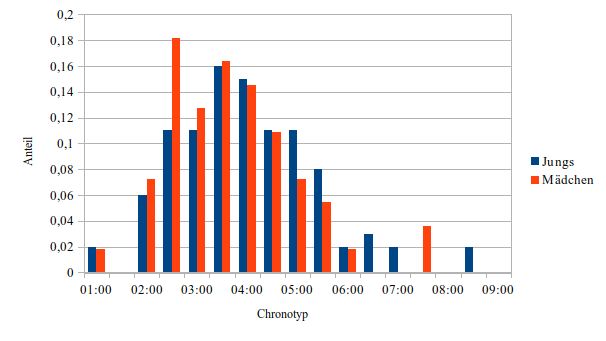
männlichweiblich
Stichprobenumfang10055
Anzahl Klassen85
Mittelwert3:59 Uhr3:42 Uhr
Varianz1,95 h²1,57 h²
Standardabweichung1,396 h1,252 h
X²6,98915,337
Statistische Signifikanz70%99,9%

Mittels t-Test kann ich nun überprüfen, ob die Mittelwerte übereinstimmen oder nicht.

\hat z = \frac{3:59 – 3:42}{\sqrt{\frac{1.95}{100}+\frac{1.57}{55}}} =\frac{0.283 \bar 3}{0.2191} =1.2926 >1.282 =z_{0.10}

Damit kann die Nullhypothese, dass die Mittelwerte der zwei Gruppen übereinstimmen, auf dem 10%-Niveau abgelehnt werden. Die hier übliche Grenze ist 1%, damit man annehmen kann, dass es sich um zwei unterschiedliche Gruppen handelt. Hier ist in einem von 10 Fällen doch kein Unterschied zwischen Mädchen und Junge. Damit kann ich über den Unterschied zwischen Mädchen und Jungen keine belastbare Aussage treffen

Zurück zur Durchführung
Zu den Ergebnissen

Leave a Reply